עצה 1: איך למצוא את היסודות של טרפז
עצה 1: איך למצוא את היסודות של טרפז
בסיסים של הטרפז ניתן למצוא במספרשיטות, בהתאם לפרמטרים שצוין. עבור אזור ידוע, גובה וצד של טרפז דו צדדי, רצף החישובים מצטמצם לחישוב הצדדים של משולש איסוסל. וגם את השימוש של רכוש של טרפז isosceles.

הוראות
1
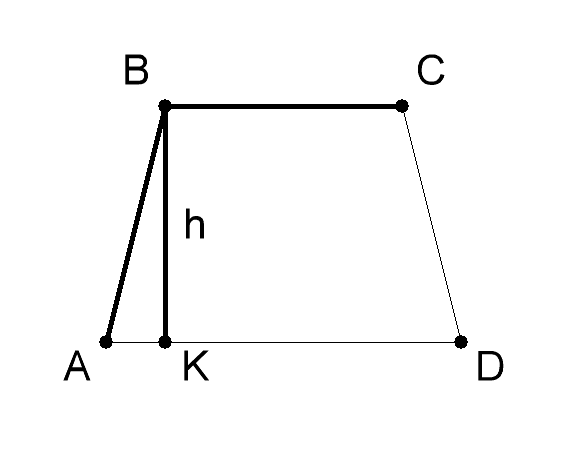
צייר טרפז דו צדדי. בהתחשב בשטח טרפז - S, גובה טרפז - ח ואת הצד - א. מנמיכים את גובה הטרפז לבסיס גדול יותר. הבסיס הגדול יותר יחולק למקטעים m ו- n.

2
כדי לקבוע את אורך שני הבסיסים (x, y), להחיל את המאפיין של טרפז דו צדדי ואת הנוסחה לחישוב שטח טרפז.
3
על פי המאפיין של הטרוזיום isosceles, קטע nשווה למחצית ההבדל בין הבסיסים x ו- y. כתוצאה מכך, הבסיס הקטן יותר של y הטרפז יכול להיות מיוצג כהפרש של הבסיס הגדול יותר, והקטע n מוכפל בשתיים: y = x - 2 * n.

4
מצא את הקטע קטן לא ידוע n. כדי לעשות זאת, לחשב צד אחד של המשולש הנכון שנוצר. המשולש נוצר על ידי גובה - h (cathet), בצד - (hypotenuse) ואת קטע - n (cathet). על פי משפט פיתגורס, הקתדרלה הלא ידועה n² = a² - h². להחליף את הערכים המספריים הידועים ולחשב את הריבוע של הרגל n. קח את שורש הריבוע של הערך המתקבל - זה אורך של קטע n.

5
תחליף ערך זה למשוואה הראשונה עבור מחשוב y. שטח טרפז מחושב על ידי הנוסחה S = ((x + y) * h) / 2. להביע את המשתנה הלא ידוע: y = 2 * S / h - x.

6
רשמו שתי משוואות שהתקבלו במערכת. החלפת ערכים ידועים, למצוא את שני כמויות לא ידוע במערכת של שתי משוואות. הפתרון המתקבל של המערכת x הוא אורך הבסיס הגדול יותר, ו- y הוא הבסיס הקטן יותר.

טיפ 2: כיצד למצוא את אורך הבסיס של הטרפז
כדי לציין כזה מרובע כמו טרפז, לפחות שלושה הצדדים שלה חייב להיות מוגדר. לכן, למשל, אנחנו יכולים לשקול בעיה שבה אורכים של אלכסונים ניתנים טרפז, וגם אחד של וקטורים של הצד לרוחב.

הוראות
1
2
שקול את המשולש עבד. אורכו של הצד AB שווה למודול של הווקטור א. נניח כי | | a = = sqrt ((ax) = 2 + (a) = 2) = a, ולאחר מכן cosφ = ax / sqrt ((גרזן) ^ 2 + (ay) ^ 2) כמו הקוסינוס המכוון של. אלכסון BD יש ארוך p, ואת המודעה הרצוי ארוך x. לאחר מכן, על ידי משפט הקוסינוס, P ^ 2 = a ^ 2 + x ^ 2-2axcosφ. או x2 2axcosφ + (a ^ 2-p ^ 2) = 0.
3
הפתרונות של משוואה ריבועית זו הם: X1 = (2acosf + sqrt (4 (a ^ 2) (cosφ) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + sqrt (a ^ 2) ((cos)) 2 (+) ^ 2) + sqrt (((a) ^ 2) (גרזן ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + p ^ 2) = AD.
4
כדי למצוא את העליונה יסודות לפנה"ס (אורכו בחיפוש אחר פתרון מסומן גם על ידי x), נעשה שימוש במודול | a = = a, וגם באלכסון השני BD = q ובקוסינוס של הזווית ABC, אשר ללא ספק שווה ל- (n-φ).
5
המשולש ABC, kאשר, כמו קודם, משפט הקוסינוס מוחל, ואת הפתרון הבא עולה. אם ניקח בחשבון ש- cos (n-φ) = cosφ, על בסיס הפתרון עבור AD, נוכל לכתוב את הנוסחה הבאה, החלפת p לפי q: BC = - a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2 ) + ((^ (^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^) ^ ^ ^ \) ^ ^ ^ ^ \ ^ ^ ^ ^ ^).
6
משוואה זו מרובעת,בהתאם, יש שני שורשים. לכן, במקרה זה נותר רק לבחור אותם שורשים בעלי ערך חיובי, שכן אורך לא יכול להיות שלילי.
7
דוגמה טרפז הצד ABCD של AB ניתנת על ידי וקטור a (1, sqrt3), p = 4, q = 6. מצא יסודות טרפזהחלטה. באמצעות האלגוריתמים שהתקבלו לעיל, אנו יכולים לכתוב: | a | = a = 2, cosφ = = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (13) 1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.
עצה 3: כיצד למצוא את גובה הטרפז
טרפז הוא מרובע, yאשר שני הצדדים מקבילים, ושני האחרים אינם. גובה הטרפז הוא קטע המצויר בין שני קווים מקבילים. בהתאם לנתונים הראשוניים, ניתן לחשב אותו בדרכים שונות.

יהיה עליך
- ידע של הצדדים, הבסיסים, קו האמצע של הטרפז, כמו גם, באופן אופציונלי, שטחו ו / או המערכת.
הוראות
1
אחת הדרכים לחשב את שטח הטרפזהוא תוצר של גובה קו מרכז. נניח שיש טרפז isosceles. לאחר מכן גובה הטרוזיום של איסופל עם בסיסים a ו- b, שטח S והיקף P יחושב כדלקמן: h = 2 x S / (P-2 x d). (ראה איור 1)
2
אם רק השטח של הטרפז ובסיסו ידועים, אז את הנוסחה חישוב גובה ניתן לגזור מן הנוסחה אזור טרפזי S = 1 / 2h x (a + b): h = 2S / (a + b).
3
נניח שיש טרפז עם נתונים כמוובאיור 1. אנו מציירים 2 גבהים, אנו מקבלים מלבן, שבו שני הצדדים הקטנים יותר הם הרגליים של משולשים זווית ישרה. תן לנו לציין את קטן עבור x. הוא נמצא על ידי חלוקת ההבדל אורך בין הבסיסים גדולים יותר. ואז, על פי משפט פיתגורס, הריבוע של גובה שווה לסכום של הריבועים של d hypotenuse ואת הרנטגן. אנו לחלץ את השורש מסכום זה ולקבל את גובה h. (איור 2)

טיפ 4: איך למצוא את הבסיסים של טרפז מלבני
דמות מתמטית עם ארבע פינות נקראת טרפז, אם זוג הצדדים המנוגדים שלה מקביל, והשני לא. הצדדים מקבילים נקראים שטח טרפז, השני - לרוחב. במלבן טרפז אחת הזוויות בצד היא ישר.
הוראות
1
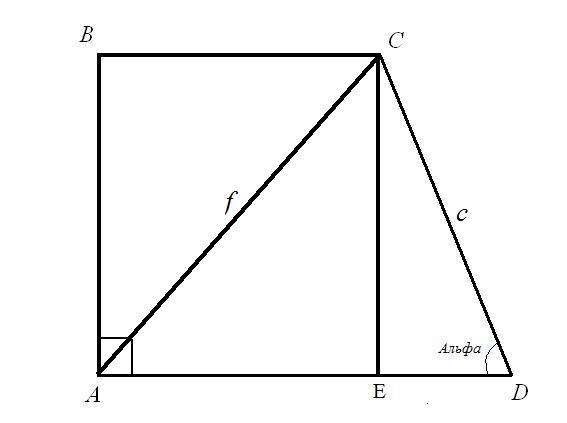
משימה 1. מצא את הבסיסים של BC ו AD מלבני טרפזאם ידוע כי אורך ה- AC = f האלכסון ידוע; אורךצדדי CD = C ואת הזווית עם זה ADC = α. פתרון: שקול את המשולש מלבני CED. ידוע hypotenuse c ואת זווית בין hypotenuse ואת הרגל של EDC. מצא את אורכי הצדדים CE ו ED: על פי הנוסחה זווית CE = CD * חטא (ADC); ED = תקליטור * cos (ADC). אז: CE = c * sinα; ED = c * cosα.
2
קחו את המשולש הנכון ACE. Hypotenuse AC ו CE ידועים לך, למצוא AE צד לפי הכלל של המשולש הנכון: סכום הריבועים של הרגליים שווה הכיכר של hypotenuse. אז: AE (2) = AC (2) - CE (2) = f (2) - c * sinα. חישוב השורש הריבועי של הצד הימני של המשוואה. מצאת את הבסיס העליון של מלבני טרפז.
3
אורך הבסיס הוא סכום אורכי השנייםמגזרים AE ו- ED. AE = שורש ריבועי (f (2) - c * sinα); * C = cosα) = AD = c * cosα) אזי: AD = שורש ריבועי (f (2) - c * sinα) + c * cosα - מצאת את הבסיס התחתון של מלבני טרפז.
4
משימה 2. מצא את הבסיסים של BC ו AD מלבני טרפזאם אורך של BD = F אלכסוני ידוע; אורךצדדי CD = C ואת הזווית עם זה ADC = α. פתרון: שקול את המשולש מלבני CED. מצא את אורכי הצדדים CE ו- ED: CE = CD * sin (ADC) = c * sinα; ED = תקליטור * cos (ADC) = c * cosα.
5
שקול את המלבן ABCE. על ידי המאפיין של המלבן AB = CE = c * sinα. שקול את המשולש הנכון עבד. על ידי המאפיין של המשולש הימני, הריבוע של hypotenuse שווה לסכום של הריבועים של הרגליים. לכן, AD (2) = BD (2) - AB (2) = f (2) - c * sinα. מצאת את הבסיס התחתון של מלבני טרפז AD = שורש ריבועי (f (2) - c * sinα).
6
לפי כלל המלבן BC = AE = AD = ED = השורש הריבועי (f (2) - c * sinα) - c * cosα מצאת את הבסיס העליון של מלבני טרפז.
עצה 5: איך למצוא את הצד הקטן של הטרפז
הבסיס הקטן יותר של הטרפז הוא אחד הצדדים מקבילים, אשר אורך מינימלי. חישוב ערך זה במספר דרכים, תוך שימוש בנתונים מסוימים.

יהיה עליך
- - מחשבון.
הוראות
1
אם שני אורכים ידועים - בסיס גדולטרפזיום ו קו האמצע - להשתמש ברכוש טרפזי לחשב את הבסיס הקטן ביותר. לדבריו, הקו האמצעי של הטרפז הוא זהה למחצית הסכום של הבסיסים. במקרה זה, הבסיס הקטן ביותר יהיה שווה להפרש של אורך כפולים של קו האמצע ואת אורך הבסיס הגדול של דמות זו.
2
אם אתה יודע פרמטרים כגון טרפז כמושטח, גובה, אורך של בסיס גדול, ולאחר מכן לחשב את הבסיס הקטן ביותר של נתון זה מבוסס על הנוסחה טרפז אזור. במקרה זה, התוצאה הסופית מתקבלת על ידי הפחתת ההפרש של האזור הכפול המצוטט וגובה פרמטר כזה כאורך הבסיס הגדול של הטרפז.
3
אורכו של הצד הקטן ביותר מלבניטרפזיום לחשב בשיטה אחרת. פרמטר זה יהיה שווה לתוצר של אורך הצד השני ואת הסינוס של הזווית החדה הסמוכה אליו. באותם מקרים, כאשר ערך הזווית אינו ידוע, משווים את צד הצד הקטן ביותר לגובה הטרפז ומחשבים אותו לפי משפט פיתגורס. הצד הקטן ביותר של הטרפז המלבני נמצא באמצעות משפט הקוסינוס: c² = a² + b²-2ab * cosα; כאשר a, b, c מייצג את הצדדים של המשולש; α היא הזווית בין הצדדים a ו- b.
עצה 6: איך למצוא את הגובה הקטן יותר של המשולש
במשולש, היחסים בין הצדדים והפינות קשורים בצורה נוקשה גם לקווים הפנימיים של הדמות - גבהים, חציונים וביסקטורים. ידיעת היחסים הללו מפשטת מאוד את פתרון הבעיות.

הוראות
1
מבין שלושת גבהים של המשולש,אשר מוריד את הגדולה של הצדדים של הדמות. כדי לראות זאת, להביע את כל שלושת גבהים של המשולש דרך ממדי הצדדים שלה ולהשוות. נניח שהצד A הוא הגדול מבין שלושת הצדדים a, b, c של משולש חד-זוויתי שרירי, הצד c הוא הקטן ביותר. אנו מציינים את גובה h בצד a, hb גובה נמשך בצד b, hc גובה לצד c. גובה מחלק כל משולש לשני משולשים מלבניים, בהם גובה זה תמיד יהיה אחד הרגליים.
2
גובה חה, נמשך לצד הגדול ביותר של,ניתן לקבוע לפי משפט פיתגורס: h² = b² - а ² או hа² = ²² - а². היכן a ו a₂ הם הקטעים שבהם הצד הוא מחולק גובה חה. כמו כן, על פי משפט פיתגורס, להביע את שני גבהים אחרים של המשולש דרך הצדדים שלה: hb ² = a²-b₁² או hb² = c²-b₂²; hc² = a²-c₁² או hc² = b²-c₂².
3
מהשוואת הנוסחאות הקובעות את הגבהיםמשולש, ברור כי היחס בין minuend ו מְחַסֵר נותן את ההבדל הקטן במונחים ha² = b² - a₁² ו ha² = s²-a₂² כמו לניכוי a₁ ו a₂ - אורכי הצד הגדול של משולש.
4
כדי לקבוע את הגובה הקטן יותר של המשולש, אתה יכולגם דרך הסינוס של הזווית הידועה של המשולש. אם על פי המצב הגדול ביותר של זוויות נתון, אז זו זווית מונחת על הצד הגדול ביותר, וממנו את הגובה הנמוך ביותר הוא נמשך. כדי למנוע חישובים מסורבלים, עדיף להביע את הגובה הרצוי באמצעות הפונקציות הטריגונומטריות של שתי הזוויות האחרות של המשולש, שכן היחס בין צד המשולש לסנטימטר של הזווית המנוגדת הוא קבוע עבור משולש נתון. לפיכך, הגובה הקטן ביותר של המשולש ha = b * SinB או ha = c * סינק, כאשר B הוא הזווית בין הצד הגדול ביותר של צד ב ו, ו- C היא הזווית בין הצד הגדול ביותר של a ואת הצד של המשולש.